Abandonar el territorio de la objetividad no es algo menor. Necesitamos buscar en otro sitio un refugio que nos dé cobijo frente a este aparente desamparo producto del fallido proyecto al que nos ha empujado la modernidad.
Cuando formulamos una explicación para dar cuenta de una experiencia, lo que
hacemos es proponer un conjunto de antecedentes conectados entre sí de una
forma tal que un observador aceptará o no la explicación conforme esté o no de
acuerdo con los criterios de validez que pone en su escuchar. En este sentido, nos
encontraremos con diversas clases de explicación llevando consigo criterios que
pueden ser místicos, religiosos, doctrinales (merced a una ideología política) o
científicos entre otros.
Pues bien, dentro de las clases de explicaciones que en nuestra modernidad
hemos cultivado y utilizado frecuentemente para dirimir quien tiene la razón en la
búsqueda de una anhelada objetividad, es el explicar basado en un razonamiento
lógico impecable; aquel que al seguir su argumentación paso a paso
supuestamente no debiese dar pie a interpretaciones que vayan más allá del hilo
conductor que propone dicha argumentación. Es la herramienta favorita del
diálogo (cuya etimología es “a través del logos”).
En lo que sigue, sin embargo, propondré una manera diferente de beneficiarse del
diálogo, no para argumentar una supuesta verdad, sino más bien para visibilizar y
aceptar nuestras legítimas diferencias. Tal como sostiene Humberto Maturana,
todo sistema lógico se basa en premisas fundamentales que son aceptadas a
priori desde una emoción de preferencia.
Así las cosas, un ejemplo de premisa fundamental aceptada a priori involucra a las
matemáticas, una disciplina de orden lógico cuyo edificio conceptual se sustenta
sobre unos cimientos denominados axiomas: proposiciones que se asumen ciertas
sin demostración; es decir, se eligen a priori. Aún así, ¿es posible a partir de un
sistema lógico dar cuenta privilegiada de alguna verdad inobjetable a pesar de
elegir arbitrariamente un conjunto de premisas a priori?
Einstein era consciente de que los supuestos eran «creaciones libres del espíritu
humano»” y aun así buscó hasta el día de su muerte una teoría unificadora que
diese cuenta de la realidad. Por otro lado, estaba suficientemente entendido desde
hacía ya bastantes siglos que efectivamente los axiomas (las premisas
fundamentales sobre las que se erigían la aritmética, la geometría y otros sistemas
matemáticos) se aceptaban a priori desde una elección arbitraria no demostrable.
Esto entregaba inseguridad, ambigüedad y un riesgo claro para el progreso de la
técnica moderna. Así, Descartes, símbolo de la modernidad, buscó afanosamente
un método que permitiese erigir el razonamiento lógico desde un cimiento
absolutamente firme para las ciencias: un fundamentum inconcussum.
Lo que no se sabía, hasta el año 1931, era que cualquiera fuesen las premisas
aceptadas a priori, nunca se podría dar fe de que el sistema lógico fuese
consistente, es decir, que no se pudiesen escapar contradicciones lógicas.
Veamos esto con un poco de historia.
Bertran Russell, connotado matemático y filósofo, dedicó una buena parte de su
vida a edificar en profundidad un sustento lógico que fundamentara la consistencia
de los conocimientos matemáticos a partir de un conjunto de axiomas. Lo anterior
quedó plasmado en una obra monumental de tres tomos llamada Principia
Mathematica. Años más tarde de haberse publicado su trabajo (en colaboración
con Alfred North Whitehead), un joven matemático de tan sólo 25 años publicó un
breve artículo –el año 1931– cuyo sugerente título era «Sobre proposiciones
formalmente indecibles de los Principia Mathematica y sistemas afines».
No obstante, las intrincadas argumentaciones de sus teoremas y quizás abusando
del lenguaje, lo que mostró Gödel en su artículo tenía que ver con la imposibilidad
de demostrar la verdad o falsedad de ciertas proposiciones aritméticas a partir de
la misma aritmética . Más aún, demostró la imposibilidad de demostrar la
consistencia de la aritmética u otro sistema lógico similar o de mayor complejidad
utilizando el mismo sistema lógico.
Resumiendo, con otras palabras, uno de los aspectos cruciales que Gödel mostró
es que un sistema matemático bajo ningún punto de vista podía demostrar,
utilizando su propia legalidad, que él mismo era un sistema impecablemente
consistente. La autorreferencia implícita terminó siendo un obstáculo insalvable.
Algo que al propio Russell le incomodaba y trató de desterrar a contrapelo en su
obra.
Visto así, junto a la publicación del artículo de Gödel, dramáticamente se ponía fin
al tan anhelado sueño de Russell –y de muchos otros connotados matemáticos
como Hilbert– de reducir las matemáticas a un cuerpo lógico consistente. El
trabajo de Kurt Gödel constituyó una de las grandes contribuciones a la lógica y
las matemáticas de los últimos siglos.
La autorreferencia ya venía inquietando a los filósofos desde la antigüedad. Para
ejemplificar los desaguisados lógicos que puede llevar un enunciado
autorreferente, veamos lo que a Epiménides, poeta y filósofo del siglo VI a.C., se
le atribuye haber afirmado:
“Todos los cretenses son mentirosos”.
Siendo Epiménides también un cretense, ¿lo que dice es verdad?
Otro ejemplo de autorreferencia lo podemos rescatar del escritor Jorge Luis
Borges. Nunca escribió novelas, sólo relatos y microcuentos en el campo de la
narrativa. Gustaba acariciar espacios y tiempos infinitos y aun así los compactaba
con elegancia y belleza:
“En Sumatra, alguien quiere doctorarse de adivino. El brujo examinador le
pregunta si será reprobado o si pasará. El candidato responde que será
reprobado…”
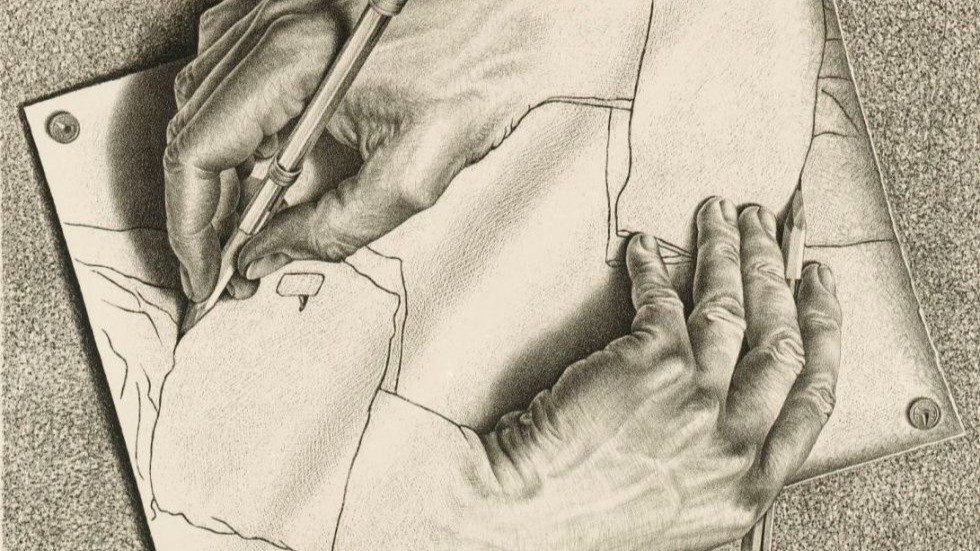
El artista holandés M. C. Escher nos da otro ejemplo de autorreferencia a través
de la circularidad de sus litografías y que ponen a prueba nuestra natural forma de
pensar lineal de causa y efecto… ¿Cuál es la causa y el efecto de la litografía «Manos Dibujando»? (Drawing Hands, fotografía que se muestra en la parte superior)
Abandonar el territorio de la objetividad no es algo menor. Necesitamos buscar en
otro sitio un refugio que nos dé cobijo frente a este aparente desamparo producto
del fallido proyecto al que nos ha empujado la modernidad.
Que no se malentienda. Muchas decisiones en una empresa son el resultado de
sofisticados formalismos lógicos como la investigación de operaciones, modelos
de valoración económica, gestión de procesos y un largo etcétera. Por supuesto
son bienvenidos y, no cabe duda, han permitido grandes saltos de productividad.
Además, nos entregan un lenguaje común para ponernos de acuerdo y evidenciar
cualquier error lógico. Lo central es estar atentos a los supuestos sobre los cuales
se basan estas herramientas. Muchas veces de manera ciega abrazamos
tendencias y modas del management y no nos damos cuenta de lo que ello
implica. Cuestionar nuestros supuestos nos lleva a innovar y a transformar la
realidad que construimos.
La invitación es, entonces, a cultivar lo que es propio de nosotros; desarrollar
nuestra propia responsabilidad ética por lo que decimos y por lo que hacemos.
Atreverse a hablar en primera persona con todo lo que ello implica: nuestras
emociones de preferencia saldrán a la luz y aquello entregará la honestidad de
explicitar lo que queremos conservar en una relación de convivencia. Es cierto,
puede que nos podamos sentir vulnerables, pero también nos entregará
responsabilidad y la maravillosa oportunidad de conocernos. Es el fin de la
objetividad, el renacer de la ética y, por supuesto, es la puerta de entrada que nos
permitirá materializar potentes transformaciones que den rienda suelta a la
creatividad.
Basado en el libro “Coherencia. Armonizando estrategia y cultura organizacional
en tiempos de incertidumbre” de Paulo Henríquez Munita.
Fuente Imagen: M. C. Escher, Manos dibujando, 1948. Litografía, Bool 355, 282 x 332 mm. Colección particular, Italia. All M. C. Escher works © 2021 The M. C. Esche



Deja una respuesta